Temperature conversions of special types

Search for more weird possibilities.

I'll start with the most familiar temperature measurements.  Here are two simple temperature conversions for you.

Fahrenheit scale

Start with Celsius.  Take 40 and add it.  Multiply by 9.  Divide by 5.  Subtract 40 from that.  Now you've got it in Fahrenheit.

Now the other way:  Start with your Fahrenheit.  Just add 40.  Take that number and multiply it by 5.  Then divide by 9.  Subtract 40 from the result.  Easy peasy.

The Fahrenheit scale is mainly used in the United States and a few other countries.  Water's freezing point is 32°F, and its boiling point is 212°F.  -459.67°F is absolute zero, the lowest temperature possible.

The Celsius scale is the most widely used temperature scale worldwide.  It's common in science and everyday life.  The freezing point of water is 0°C, and the boiling point is 100°C.  The absolute zero temperature is -273.15°C.

Kelvin (K): This is an absolute temperature scale that's used in science and thermodynamics.  Temperature differences and energy calculations are common uses for it.  Kelvin scale starts at absolute zero, where 0 K represents no thermal energy.  A Kelvin increment is the same size as a Celsius degree increment, so an increase of 1 Kelvin is the same as an increase of 1 Celsius.

Rankine is another temperature scale used in some engineering applications, especially in the US.  With absolute zero being 0 Rankine (R), the Rankine scale is based on the Fahrenheit scale.  Rankine scale increments are the same size as Fahrenheit degrees.  Although Rankine isn't as common as Celsius, Fahrenheit, or Kelvin, it's still used in specific engineering and scientific contexts, especially in the US.

Absolute zero is the lowest temperature on any scale.  All molecular motion stops at absolute zero, and substances reach their lowest possible energy state.  The point where no heat can be extracted from a system is the point of minimum thermal energy.  In scientific and thermodynamic calculations, absolute zero serves as the starting point for measuring temperature.

Special Temperature conversions used in meteorology

Weather forecasters use conversions to find the average temperature of any upper layer.  They convert an individual temperature profile into a typical value for that atmospheric layer.

You can do this with a tephigram or skew-t chart.  You can use layer averaging or other things like mixing ratios. But why?  Check out these examples.

1) The type of precipitation is determined by the average temperature.  It could be rain, snow, hail, or something else.

2) One can estimate atmospheric turbulence near the ground by averaging potential temperatures.  That's especially true if it's sunny!

3) Check out one of these charts for the dewpoint curve.  At low elevations, it shows that the air mixes well in this layer if it slopes up to the right.  Warmer air moves up and cooler air moves down because of this mixing. As a result, the temperature in different layers of the atmosphere stays the same and vapour in the air are dispersed.  This is a handy tool for forecasting convection, turbulence and storms.

4) Let's go back to the good old wet-bulb potential temperature.  Here's another temperature conversion.  It's great for finding temperatures after rain or downbursts.  We can also figure out what type of air mass it is.

Here is how you can do it

Firstly, by eyeball.  This is a quick, crude way to convert temperatures.  The person needs to have enough skill to average this way.

Here's the formal method.  Decide what layer you need an average for.  Decide what parameter (isotherm, temperature, etc) you need to average.  Find a value for that parameter, by trial and error if necessary, that meets this condition:

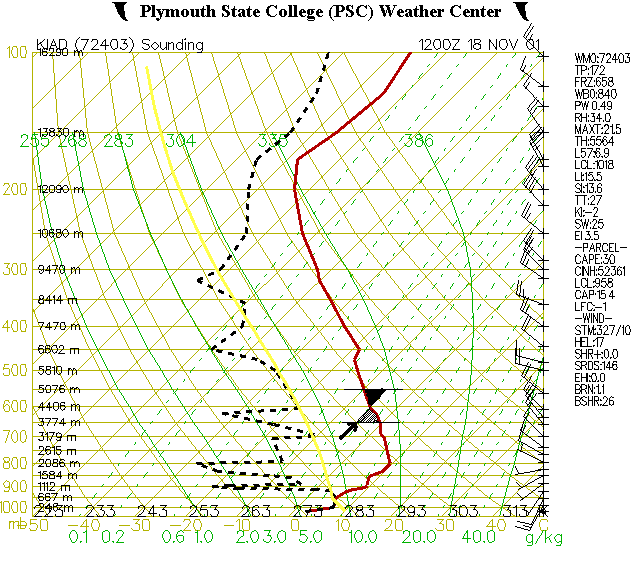
From the top of your chosen layer to the bottom, draw a single line or curve so that one side of the radiosonde curve has about the same area as the other side.  Take a look at this American example...

Analyzing Skew-T Log-P charts

Here's an equal area technique.  The black area above the red line is roughly equal to the grey area below.  With it, we figure the average temperature between 550 millibars and 650 millibars (3774 meters above sea level and 5076 meters above sea level) was -5 degrees Celsius.  Our average temperature value is halfway between 0 and -10, as you can see from the straight yellow isotherms sloping down to the left.

Besides the temperature conversions, notice the hockey sticks on the right in this sample drawing.  These are in a lot of plots.  Wind speed and direction are displayed at corresponding heights.  We get this data from the balloon's trajectory, not stationary wind meters.

A long spike means 10 knots, which is about 11 mph or 19 km/h, a half spike means 5 and a black flag (pennant-shaped, not shown in this example) means 50.  In addition, the shaft angle shows the upwind direction, with most of these in the picture above showing westerly or northwest winds near the surface.

Go back from Temperature Conversions to the Chasing Storms webpage. If you have anything to add, please leave your comment right here.

We are NOT Geeks

At least that's what some people think. Do you think math helps us to understand our world? Succeed at work? Use a computer?

You bet. That reminds me, it can help make you a better gambler if you're so inclined.

What's the most important thing math helps you with?

First part of this Equation: a title

Show me the Money...I mean the story. [ ? ]

Close Help It's easy to do. Just type!...no registration or login required. Your story will appear on a Web page exactly the way you enter it here. You can wrap a word in square brackets to make it appear bold. For example [my story] would show as my story on the Web page containing your story. I then add my own comments first, before others get a chance. Then you get to see what THEY have to say. TIP: Since most people scan Web pages, include your best thoughts in your first paragraph.

Got a Diagram, a sketch, a drawing or a photo?[ ? ]

Close Help Do you have one of these to add? Great idea! Click the button and find it on your computer. Then select it. Only .jpg's work here.

Add a Picture/Graphic Caption (optional)  

Click here to upload more images (optional)

Add a Picture/Graphic Caption (optional)  

Add a Picture/Graphic Caption (optional)  

Add a Picture/Graphic Caption (optional)  

Author Information (optional)

To receive credit as the author, enter your information below.

Your Name	(first or full name)
Your Location	(e.g., City, State, Country)

Submit Your Contribution

• Check box to agree to these  submission guidelines.
• I am at least 16 years of age.
• I understand and accept the privacy policy.
• I understand that you will display my submission on your website.

(You can preview and edit on the next page)

What Other Great Mathemeticians Have Said...

Click below to see contributions from other visitors to this page...

Saturday air 
how is climate on saturday? Barry's Response - Saturday air? Climate on a particular day of the week? An interesting situation. I will start …

Math and Statistics Not rated yet
i just love math.. but statistics.. hmmm i almost failed my statistics exam. :) But then again... you cannot do anything in life without statistics and …

More specific details Not rated yet
Okay, this is alright. Of course people can understand, but just reading all that words makes me so dizzy. To be honest, I'd rather see more + and - and …

Math can be useful in determining truth vs perception Not rated yet
Math can be very useful when trying to make a decision that involves money, or time and distance, or building, or many other things. We can "feel" or …

Weather math Not rated yet
This description moves a little too quickly and might use too many English idioms ("eyeballing it") for younger readers to follow along. I do data visualization …

There are 10 types of people in the world... Not rated yet
Those who understand binary and those who don't. I use basic math algorithms daily when writing code snippets for my customers. I often think back on …

Click here to write your own.

#31

Search this site for more information now.

Here are some temperature conversions you may not have seen before...

Temperature conversions for scientists - a new way to look at temperatures.

Do you have concerns about air pollution in your area??

Perhaps modelling air pollution will provide the answers to your question.

That is what I do on a full-time basis.  Find out if it is necessary for your project.

Have your Say...

on the StuffintheAir         facebook page

Other topics listed in these guides:

The Stuff-in-the-Air Site Map

And, 

See the newsletter chronicle. 

Thank you to my research and writing assistants, ChatGPT and WordTune, as well as Wombo and others for the images.

GPT-4, OpenAI's large-scale language generation model (and others provided by Google and Meta), helped generate this text.  As soon as draft language is generated, the author reviews, edits, and revises it to their own liking and is responsible for the content.